SSA按照教材上的讲,肯定是做不了的。但是也有特殊情况,那就是HL——两个直角三角形对应斜边相等和一对直角边相等,就可以证明两个三角形全等了。可是情况不止这些,可以看下面这一题。
如图,在ΔABC与ΔDEF中,AC=DF,BC=EF,∠A=∠D,∠B、∠E为钝角。求证:ΔABC≌ΔDEF
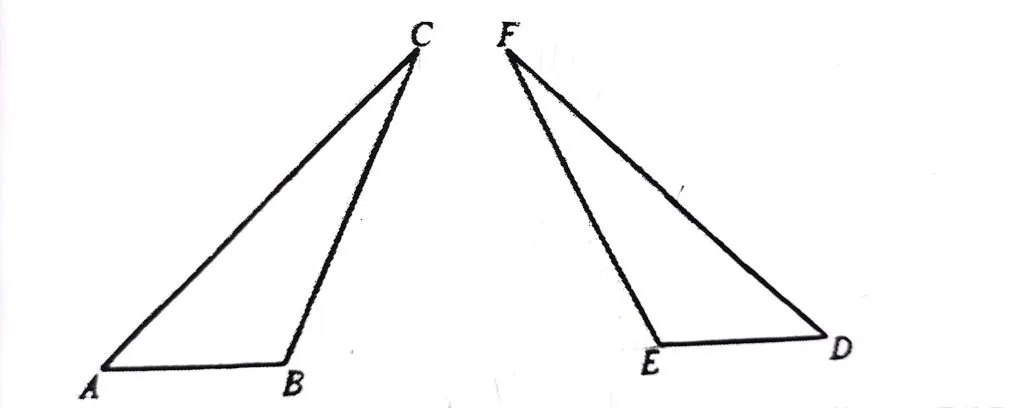
虽然有两条边和一个角对应相等,但这个角并不是两边夹角,所以不能直接证明。
因此我们可以尝试延长两个三角形的底边并在上面作高,来构造AAS。
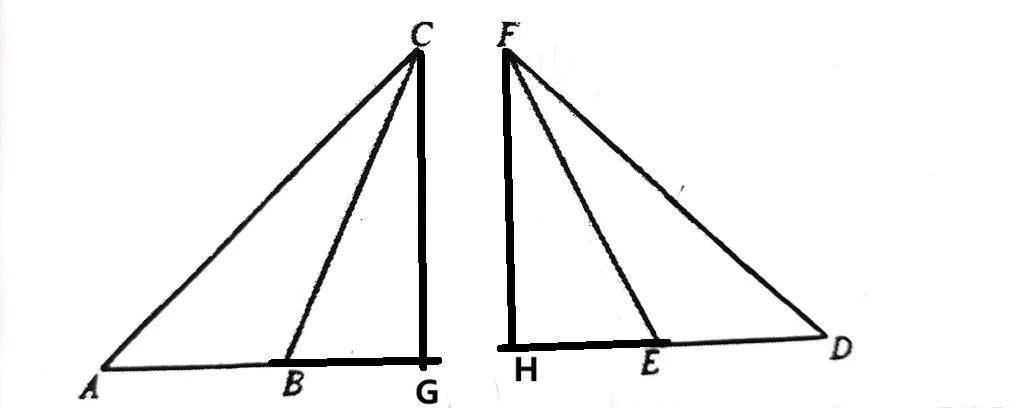
证:作AB延长线⊥CG,垂足为G;作DE延长线⊥FH,垂足为H。
在ΔACG与ΔDFH中
∠A=∠D
∠BGC=∠EHF
AC=DF
∴ΔACG≌ΔDFH
∴CG=FH AG=DH
在RtΔCGB与RtΔFHE中
CB=FE
CG=FH
∴RtΔCGB≌RtΔFHE
∴BG=EH
∴AB=DE
在ΔABC与ΔDEF中
AB=DE
AC=DF
BC=EF
∴ΔABC≌ΔDEF
Q.E.D.
这是一个笔记,拓展题挺喜欢SSA的。

让我看到了吧?学到了。
你们是不是没事干。