受力分析初中基本上就是被扔一边的,现在考试就考画图题和一小题,但实际上很重要。
步骤
1.先分析重力。若有质量,找重心,画出竖直向下的重力
2.分析弹力。找接触,判断是否有挤压。
3.分析摩擦力。找弹力,判断是否有相对运动或趋势。
4.判断合力(矩)是否为零。若然,结束;不然,则回到步骤2。
质心的受力分析
重力
重力需要注意题目有没有提及物体为轻质,没有的话需要寻找重心。
对于质量为m的物体,其所受重力G为mg。其中,g为重力常数(重力加速度),取9.8m/s^2
对于质量分布均匀、形状规则的物体,其重心位置在其几何中心。
对于两个质量分别为m_1, m_2的物体,两物体的重心距离为L,其所受的总重力为(m_1+m_2)g的等效作用点就是这个系统的重心。用无质量的硬杆将两个物体连接并选一支点使其水平平衡,这一支点就是这两个物体的等效重心。
弹力
弹力的产生需要有接触,但接触了不一定会有弹力的产生。因此需要判断。此外,弹力方向法向。
现在来分析弹力。分析弹力,先找接触,然后判断其方向,再判断其存在是否合理。再此过程中,可以先假设这一弹力的存在,这时会不会与题中的运动状态不符。若符合,则弹力存在;反之,不存在。
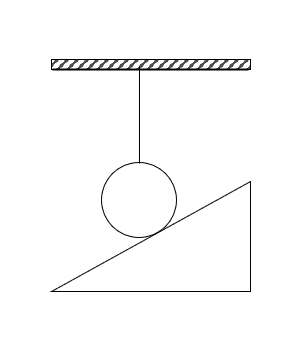
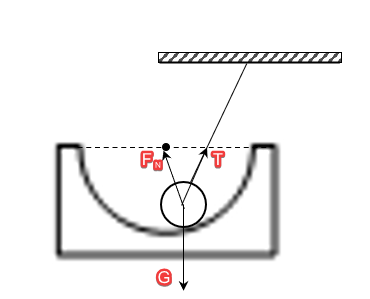
在图1中,绳子方向垂直于水平面,斜面与小球接触。小球显然受到重力和绳子的弹力,竖直方向平衡,除此之外似乎还存在一个来自斜面的支持力。不妨假设这个力的存在,由于竖直方向的平衡,这个力会使其运动不可能。因此,该物体只受竖直方向上的力。
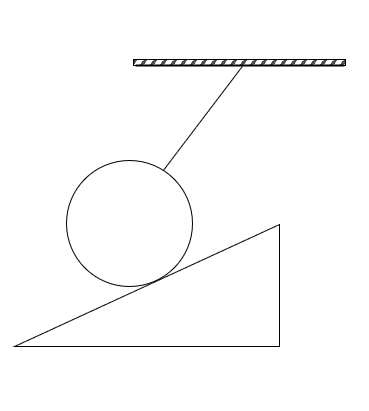
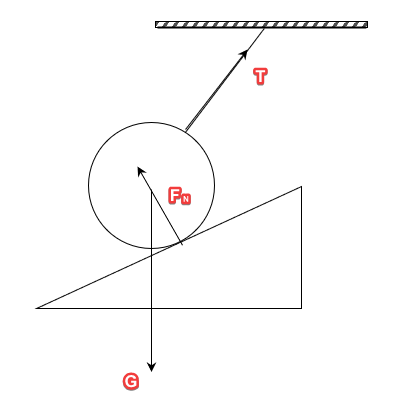
在图2中,情况有所改变,绳子不再是竖直向下的了,但其作用线始终过圆心。同图1,小球还是受到重力G、绳子的弹力T。但是,这两个力不足以平衡小球,因为弹力T有向上和向右的作用。此时,就需要斜面的支持力F_N来平衡了,方向指向球心。受力分析如下图所示。
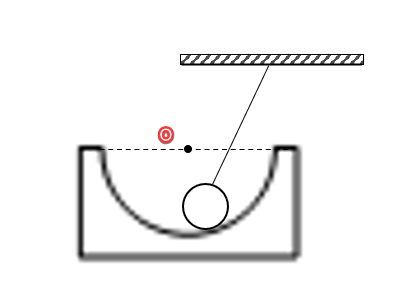
在图3中,有一被细绳拴着的小球,与一半圆槽O接触。小球一定受到一个重力、绳子的弹力和半圆槽的支持力。支持力的方向是法向的,因此应当指向半圆的曲率中心,如下图。
摩擦力
摩擦力分为滑动摩擦、滚动摩擦(不讨论)和静摩擦,摩擦力的产生必须要有弹力的存在,方向与相对运动或相对运动趋势相反,作用于接触面。接触面的种类由两个物体的物质种类、粗糙程度共同决定。
大量实验探究表明:
在接触面材质相同的情况下,滑动摩擦力与接触面所受支持力大小成正比,即F_f=\mu F_N。
质量一定的物体在同种接触面上,最大静摩擦等于滑动摩擦力,即f_{max}=F_f
最简单的就是斜面上的物块,定量分析一下。
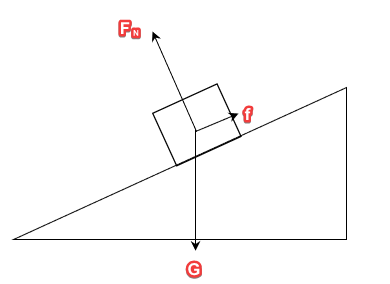
在图4中,倾角为\theta的斜面有一重为G的物块,且接触面粗糙。由此,我们可以得到物块受到三个力的作用:垂直于接触面向上的支持力F_N、沿斜面向上的摩擦力f与竖直向下的重力G。这三个力可以构成一个矢量直角三角形。
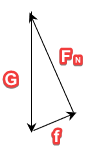
由斜面倾角为\theta,可知\vec{G}与\vec{F_N}之间的夹角也为\theta。通过直角三角比可以知道,F_N=Gcos \theta,f=Gsin \theta。
图2中,绳子延长线是过小球球心的,若不然呢?
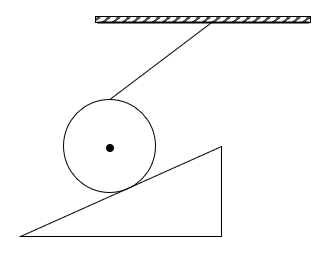
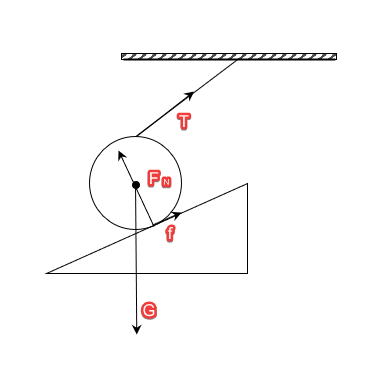
如图5,一轻绳悬着一球且其作用线不经过球心,球静止在一斜面上。和图2一样,受到重力G、来自斜面的支持力F_N与绳子的弹力T。可仅有此三个力,以球心为支点,球会顺时针旋转。而此时静止不动,说明存在一个与运动趋势相反的摩擦力f,且作用域球与斜面的接触面上。完整受力分析如下图。
杆的受力分析
杆的受力分析相较于质心的受力分析稍微复杂。在杆的受力当中,力不可以平行于作用线平移,因为这会导致好像平衡,其实不然,杆的平衡得寻找支点判断力矩和是否为零。
对于杆的受力,有一特点,有时可以方便分析:两力共线,三力的作用线共点。三力的作用线可以看作是三组共点力各自合力的作用线,不一定是三个力。
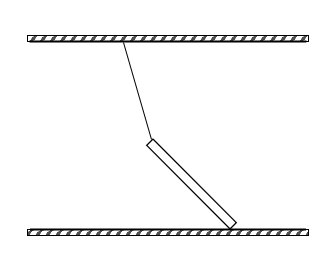
如图六,有一重杆挂于绳子上,静止于水平面。首先可以得到的力是重力、来自绳子的弹力和水平面的摩擦力,如下图。
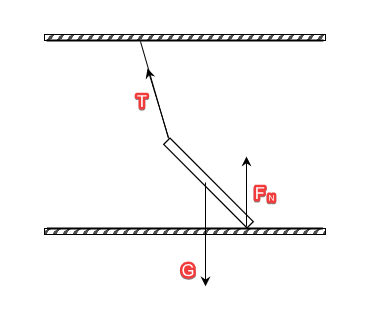
三力作用线不共点,不平衡,因此水平面必定有摩擦力。
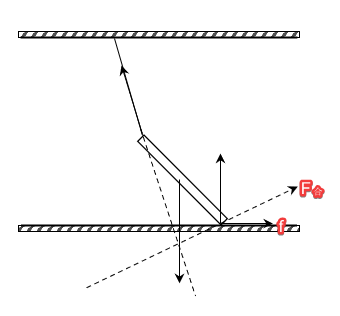
弹力T作用线与重力G交于O,再联O与支持力F_N的作用点可以得到F_N与摩擦力f的合力F_合的方向,进而得到摩擦力f水平向右。所以有图6.2。

受力分析在物理学里面是相对很有意思的,我上学那会儿就物理学的不好(´இ皿இ`),加油加油
总结不错,望学习进步,学有所成。